with friends like these
— 焉知非鱼http://blogs.perl.org/users/damian_conway/2019/08/with-friends-like-these.html
C-o-rr-a-ll-i-n-g d-i-tt-o-e-d l-e-tt-e-r-s
我本打算本周重点关注第20周挑战的第一个任务……但我能说什么呢?这个任务是把一个在命令行中指定的字符串分解成相同的字符:
"toolless" → t oo ll e ss
"subbookkeeper" → s u bb oo kk ee p e r
"committee" → c o mm i tt ee
但是这在 Raku 中就是小菜一碟:
use v6.d;
sub MAIN (\str) {
.say for str.comb: /(.) $0*/
}
或者使用更优雅的方式:
.say for $str.comb: /\w+ % <same>/
而在 Perl 中也几乎一样简单:
use v5.30;
my $str = $ARGV[0]
// die "Usage:\n $0 <str>\n";
say $& while $str =~ /(.) \1*/gx;
这这两种情况下, 正则表达式只是简单地匹配任何字符((.)), 然后将相同的字符($0 或 \1)重新匹配零次或多次(*)。这两个匹配操作(str.comb 和 $str =~)都产生一个匹配的字符串列表, 然后我们输出每个字符串(.say for... 或 say $& while...)。
由于这两种情况都没什么好说的了,我反而把注意力转移到第二个任务上:找到并打印第一对友好数。
朋友的朋友就是敌人 #
友好数一对整数,每对整数都有一组合适的除数(即被每个较小的数整除)碰巧加起来是另一个数。
例如 1184 可以被 1, 2, 4, 8, 16, 32, 37, 74, 148, 296, 和 592 整除; 1+2+4+8+16+32+37+74+148+296+592 之和为 1210。同时, 数字 1210 被 1, 2, 5, 10, 11, 22, 55, 110, 121, 242 和 605 整除; 1+2+5+10+11+22+55+110+121+242+605 的和是……你猜对了……1184。
这样的数字对是不常见的。前1万个整数中只有5个,10万以下只有13个,100万以下只有41个。而越往后,它们就越稀少:小于1万亿的这种数对只有7554对。渐进地,它们在正整数中的平均密度趋于零。
还没有已知的通用公式来寻找友好数,尽管 9 世纪的伊斯兰学者 بت بن ثاقره 确实发现了一个部分方程, 欧拉(当然!) 随后在 900 年后改进了这个公式。
所以他们很罕见,而且他们是不可预测的……但他们并不是特别难找。
在数论中, 给出 N 的所有正除数之和的函数(即"有限制的除数函数")表示为 𝑠(N):
sub 𝑠 (\N) { sum divisors(N) :proper }
末尾的 :proper 是一个"副词修饰符",应用于对 divisors(N) 的调用,告诉函数只返回合适的除数(即从列表中排除 N 本身)。
还有,是的,我们用 Unicode 斜体 𝑠 作为函数名。因为我们可以。
一旦我们定义了限制性除数函数,我们就可以简单地遍历从1到无穷大的每一个整数i,找到 𝑠(i),然后检查这个数的除数之和(即 𝑠(𝑠(i))) 是否与原数相同。如果我们只需要找到第一对友好数,那就可以了。
for 1..∞ -> \number {
my \friend = 𝑠(number);
say (number, friend) and exit
if number != friend && 𝑠(friend) == number;
}
这输出:
(220, 284)
但为什么要停留在一个结果上呢?在不难发现所有友好数的情况下:
for 1..∞ -> \number {
my \friend = 𝑠(number);
say (number, friend)
if number < friend && 𝑠(friend) == number;
}
请注意,由于数字之间的友好关系(根据定义)是对称的,我们将 number != friend 测试改为 number < friend……以防止循环将每对数字打印两次:
(220, 284)
(284, 220)
(1184 1210)
(1210 1184)
(2620 2924)
(2924 2620)
(et cetera)
(cetera et)
缺少的内置 #
这个故事就这样结束了,除了一个小问题:有些出人意料。
Raku 并没有内置我们需要的除数来实现 𝑠 函数。所以我们必须自己建立一个。事实上,我们要建立相当多的除数…
一个整数的除数是指所有可以除以整数而不留余数的整数。这包括数字本身和整数1。一个数的"正除数"是指除它本身以外的所有被除数。一个数的"非平分除数"是除它本身或1以外的所有除数。也就是:
say divisors(12); # (1 2 3 4 5 6 12)
say divisors(12) :proper; # (1 2 3 4 5 6)
say divisors(12) :non-trivial; # (2 3 4 5 6)
上面的第二种和第三种选择,加上时髦的副词修饰符,其实只是普通的除数调用的语法糖,但多了一个命名参数:
say divisors(12); # (1 2 3 4 5 6 12)
say divisors(12, :proper); # (1 2 3 4 5 6)
say divisors(12, :non-trivial); # (2 3 4 5 6)
在 Raku 中,最简单的方法是使用多重分派来实现那种"副词"函数,每种特殊情况都有一个唯一的必需命名参数:
multi divisors (\N, :$proper!) { divisors(N).grep(1..^N) }
multi divisors (\N, :$non-trivial!) { divisors(N).grep(1^..^N) }
在这些特殊情况下的除数中,我们只需调用函数的常规变体(即 divisors(N)),然后 grep 出不需要的端点。
..^ 运算符产生的范围是排除自己的上限,而 ^..^ 运算符产生的范围是排除它的两个边界(是的,也有一个 ^.. 变体只排除下限)。
因此,当指定 :property 选项时,我们会过滤 divisors(N) 返回的完整列表,以省略数字本身(.grep(1...^N))。同样,当包含 :non-trivial 选项时,我们也会排除两个极值(.grep(1^..^N))。
但是原始的未过滤的除数列表呢?我们首先要怎么得到呢?
生成一个数 N 的完整除数列表的天真方法,也就是所谓的"试除",就是简单地遍历从1到N的所有数字,保留所有那些除以N而没有余数的数字……这很容易测试,因为 Raku 有 %% is-divisible-by 运算符:
multi divisors (\N) {
# Track all divisors found so far...
my \divisors = [];
# For every potential divisor...
for 1..N -> \i {
# Skip if it's not an actual divisor...
next unless N %% i;
# Otherwise, add it to the list...
divisors.push: i;
}
# Deliver the results...
return divisors;
}
只不过我们不是穴居人,我们不需要像这样把棍子揉在一起,也不需要用脚趾头数数来做数字理论。我们可以更优雅地得到同样的结果:
multi divisors (\N) { (1..N).grep(N %% *) }
在这里,我们简单地过滤潜在的除数列表 (1...N),只保留那些均匀地除以 N 的除数(.grep(N %% *))。N %% * 测试是创建一个 Code 对象的简写,这个对象接受一个参数(用 * 表示)并返回 N %% 的参数。换句话说,它通过将 infix %% 运算符的第一个操作数预先绑定到 N 上,创建了一个单参数函数。如果这对你来说在语法上过于华丽,我们也可以将它写成一个显式的 %% 运算符预先绑定:
(1..N).grep( &infix:<%%>.assuming(N) )
…或者作为一个 lambda:
(1..N).grep( -> \i { N %% i } )
…或者作为一个匿名的子例程:
(1..N).grep( sub (\i) { N %% i } )
…或者作为一个命名子例程:
my sub divisors-of-N (\i) { N %% i }
(1..N).grep( &divisors-of-N )
Raku 的目标是让我们用我们认为最方便、最舒适、最容易理解的任何一种符号来表达自己。
从问题的根源入手 #
很难想象还有比这更简单的解决找除数问题的方法:
multi divisors (\N) { (1..N).grep(N %% *) }
但也很难想象还有效率更低的。例如,为了找到数字2001的8个被除数,我们必须检查所有2001个潜在的被除数,这就浪费了 99.6% 的精力。即使是像2100这样的数字, 它有36个被除数, 我们仍然浪费了超过 98% 的 1..N 序列。而且数字越大,被除数的相对数量越少,找到它们的时间也越长。
一定有更好的方法。
当然,是有的。我们能做的最简单的改进是早在1202年由斐波那契在他的巨著自由女神中首次发表的。我们首先观察到,一个数字的除数总是以互补的方式出现,这对除数相乘产生数字本身。例如,99 的除数是:
1 3 9
99 33 11
…而 100 的除数是:
1 2 4 5 10
100 50 25 20 10
…而 101 的除数是:
1
101
注意,在每一种情况下,顶行除数总是包含不大于原数平方根的"小"整数。而底行则完全由 N 除以相应的顶行除数组成。所以我们可以通过搜索 1..sqrt N 的范围找到一半的除数(只需 O(√N)步),然后通过从 N 中减去列表中的每个元素找到另一半(也只需 O(√N) 步)。在 Raku 中,这看起来像这样:
multi divisors (\N) {
my \small-divisors = (1..sqrt N).grep(N %% *);
my \big-divisors = N «div« small-divisors;
return unique flat small-divisors, big-divisors;
}
div 运算符是整数除法,把双角放在它的周围,使它成为一个向量运算符,将 N 除以小除数列表中的每一个元素。flat 是需要的,因为小除数和大除数中的两个列表对象在 Raku 中不会自动"展平"成一个列表。unique 是需要的,因为如果 N 是一个完美的平方数,否则我们会得到它的平方根的两个副本(就像上面 100 的除数对中的 10/10 的例子)。
从大处着想 #
很高兴我们能够如此轻松地将 O(N) 算法改进为 O(√N),但即使如此也只能做到这一步。除数函数的性能直到 divisors(10⁹),在 0.1 秒以下完全可以接受,但在这之后开始迅速下降:
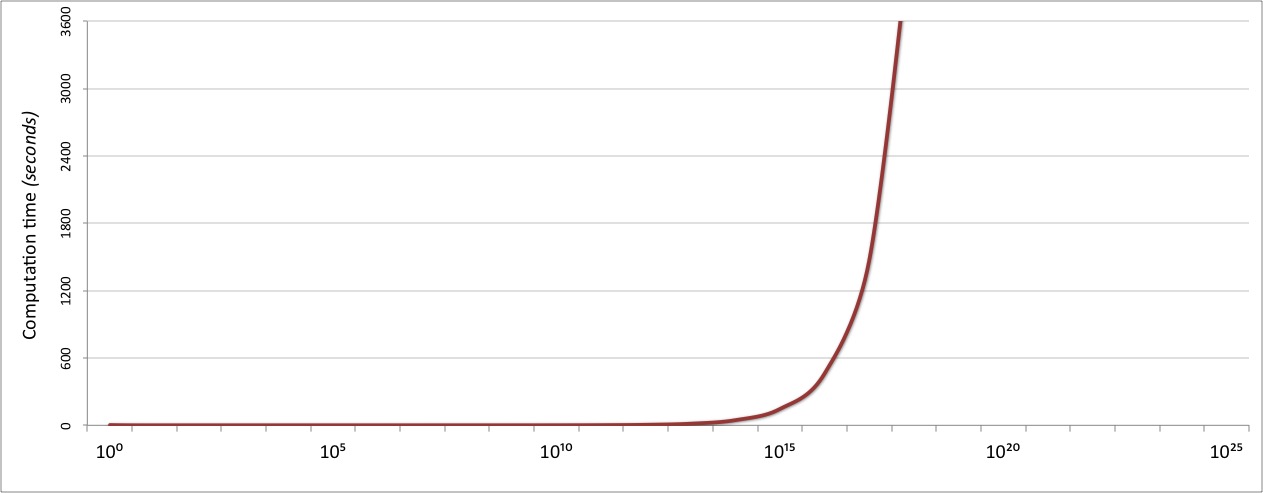
如果我们希望我们的函数可以用于非常大的数字,我们需要一个更好的算法。 而令人高兴的是,密码学的世界(它沉迷于对数字进行分解)提供了大量的替代技术,从仅仅是非常复杂的技术到积极的长生不老的技术都有。
其中一个比较容易理解(和编码!)的方法是 Pollard 的 𝜌 算法,几年前我在 Perl 会议的主题演讲中简单解释过这个算法。而 Stephen Schulze 随后在一个名为 Prime::Factor 的 Raku 模块中把它作为 prime-factors 函数提供出来。
我不打算在这里解释 𝜌 算法,甚至不打算讨论 Stephen 对它的出色实现……不过绝对值得探索这个模块的代码,尤其是那个使用 $n gcd 6541380665835015 来即时检测数字的质因数是否小于44的崇高捷径。
可以说,这个模块很快就找到了所有大数的质因数。例如,我们之前的 divisors 实现需要5秒左右才能找到1万亿的除数,而 prime-factors 函数在 0.002 秒内就能找到这个数的质因数。
唯一的问题是:一个数的质因数和它的除数不一样。1万亿的除数是所有被它偶数除的数。也就是:
1, 2, 4, 5, 8, 10, 16, 20, 25, 32, 40, 50, 64, 80, 100,
125, 128, 160, 200, 250, 256, 320, 400, 500, 512, 625,
640, 800, 1000, 1024, 1250, 1280, 1600, 2000, 2048, 2500,
[...218 more integers here...]
10000000000, 12500000000, 15625000000, 20000000000,
25000000000, 31250000000, 40000000000, 50000000000,
62500000000, 100000000000, 125000000000, 200000000000,
250000000000, 500000000000, 1000000000000
相反,一个数的质因数是唯一的(通常是重复的)质数集,可以将 它们相乘以重新组成原来的数。对于1万亿这个数字,这个唯一的质数集是:
2,2,2,2,2,2,2,2,2,2,2,2,5,5,5,5,5,5,5,5,5,5,5,5
…因为:
2×2×2×2×2×2×2×2×2×2×2×2×5×5×5×5×5×5×5×5×5×5×5×5 → 1000000000000
为了找到一对友好数,我们需要除数,也需要质因数。幸运的是,从另一个中提取一个并不难。乘以完整的质因数列表,就会产生原数,但如果我们选择质因数的各种子集来代替:
2×2×2×2×5×5×5 → 2000
2×2×2×2×2×2×2×2 → 256
2×5×5×5×5 → 1250
…那么我们就会得到一些实际的除数。而如果我们选择质因数的幂集(即每一个可能的子集),那么我们就会得到每一个可能的除数。
所以,我们需要做的就是将质因数产生的完整列表,生成该列表中元素的每一个可能的组合,将每个组合的元素相乘,只保留唯一的结果。这一点,在 Raku 看来,就是:
use Prime::Factor;
multi divisors (\N) {
prime-factors(N).combinations».reduce( &[×] ).unique;
}
.combinations 方法产生了一个列表,其中每个内部列表是原始质因数列表的一些唯一子集的一个可能的组合。类似于:
(2), (5), (2,2), (2,5), (2,2,2), (2,2,5), (2,5,5), ...
».reduce 方法调用是 “fold” 操作 的一种向量形式,它在调用它的列表的每个元素之间插入指定的操作符。在本例中,我们通过 &infix:<×> 运算符插入中缀乘法……我们可以将其缩写为:&[×]。
所以,我们得到的东西像这样:
(2), (5), (2×2), (2×5), (2×2×2), (2×2×5), (2×5×5), ...
然后我们只需通过最后调用 .unique 来剔除所有重复的结果。
尽可能的简单……但不能再简单了! #
然后我们测试我们闪亮的新的基于 prime-factor 的算法。然后哭着发现,它比我们最初的试分法慢了很多。
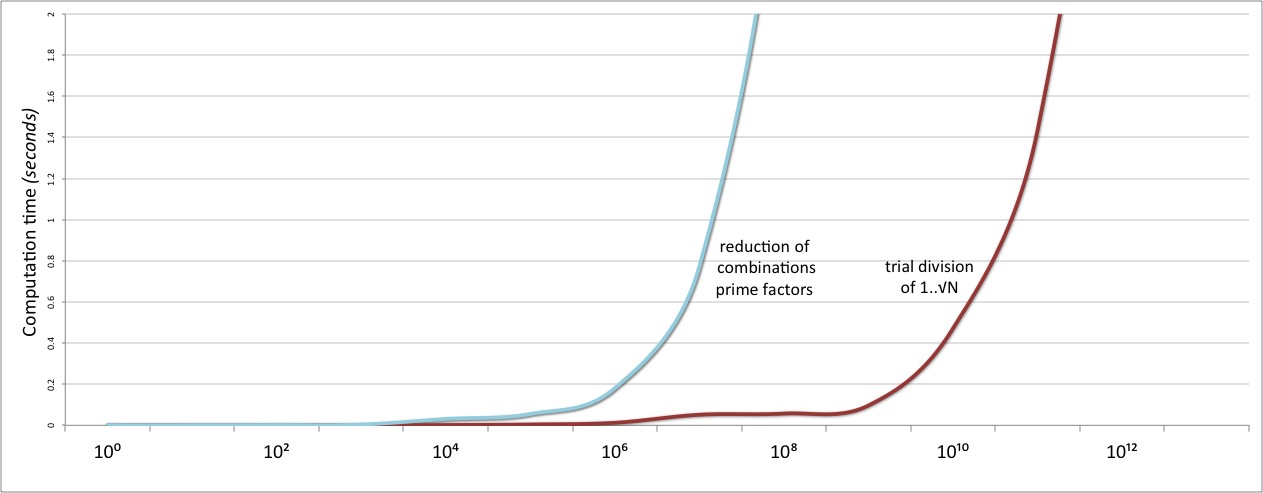
这里的问题是,.combinations 方法的使用在某些情况下会导致组合爆炸。我们通过取所有可能的质因子集,找到了完整的除数集:
2×2×2×2×2×2×2×2×2×2×2×2×5×5×5×5×5×5×5×5×5×5×5×5 → 1000000000000
2×2×2×2×5×5×5 → 2000
2×2×2×2×2×2×2×2 → 256
2×5×5×5×5 → 1250
但这也意味着,我们采取了这样的子集:
2×2×2 → 8
2×2×2 → 8
2×2×2 → 8
2 ×2 ×2 → 8
事实上,我们取了220个不同的 2×2×2 子集。更不用说495个 2×2×2×2 子集,792个 2×2×2×2 子集,等等。总的来说,1万亿的24个质因数产生了 2²⁴ 个不同的子集的幂集,我们再将其缩小到只有168个不同的除数。换句话说,.combinations 必须建立并返回一个包含 16777216 个子集的列表,».reduce 必须处理其中的每一个子集,之后,.unique 会立即丢弃其中的 99.999%。显然,我们需要一种更好的方法来将因子组合成除数。
而且,令人高兴的是,有一个。我们可以重写乘法:
2×2×2×2×2×2×2×2×2×2×2×2×5×5×5×5×5×5×5×5×5×5×5×5 → 1000000000000
…为一个更紧凑的:
2¹² × 5¹² → 1000000000000
然后我们观察到,只要改变两个质数的指数,从零到最大允许值(每种情况下都是12),就可以得到所有唯一的子集:
2⁰×5⁰ → 1 2¹×5⁰ → 2 2²×5⁰ → 4 2³×5⁰ → 8 ⋯
2⁰×5¹ → 5 2¹×5¹ → 10 2²×5¹ → 20 2³×5¹ → 40 ⋯
2⁰×5² → 25 2¹×5² → 50 2²×5² → 100 2³×5² → 200 ⋯
2⁰×5³ → 125 2¹×5³ → 250 2²×5³ → 500 2³×5³ → 1000 ⋯
2⁰×5⁴ → 625 2¹×5⁴ → 1250 2²×5⁴ → 2500 2³×5⁴ → 5000 ⋯
⋮ ⋮ ⋮ ⋮ ⋱
一般来说,如果一个数有质因数 pℓᴵ × pₘᴶ × pₙᴷ,那么它的完整除数集就由 pℓ⁽⁰‥ⁱ⁾ × pₘ⁽⁰‥ʲ⁾ × pₙ⁽⁰‥ᵏ⁾ 给出。
也就是说,我们可以这样找到它们:
multi divisors (\N) {
# Find and count prime factors of N (as before)...
my \factors = bag prime-factors(N);
# Short-cut if N is prime...
return (1,N) if factors.total == 1;
# Extract list of unique prime factors...
my \pₗpₘpₙ = factors.keys xx ∞;
# Build all unique combinations of exponents...
my \ᴵᴶᴷ = [X] (0 .. .value for factors);
# Each divisor is pₗᴵ × pₘᴶ × pₙᴷ...
return ([×] .list for pₗpₘpₙ «**« ᴵᴶᴷ);
}
我们得到了和上一个版本一样的质因子列表(prime-factors(N)),但现在我们将它们直接放入一个 Bag 数据结构中(bag prim-factors(N))。一个"bag"是一个整数加权集:一种特殊的哈希,其中键是列表的原始元素,值是每个不同值出现次数的计数(即它在列表中的"权重")。
例如,9876543210 的质因子是(2, 3, 3, 5, 17, 17, 379721)。如果我们把这个列表放到一个袋子里,我们得到的等价物是:
{ 2=>1, 3=>2, 5=>1, 17=>2, 379721=>1 }
因此,将质因数列表转换为一个袋子,我们就有了一个简单而有效的方法来确定所涉及的唯一质数,以及每个质数必须升到的幂。
然而,如果在所得的袋子中只有一个质数键,而其对应的数是1,那么原数本身一定是那个质数(升到1的幂)。在这种情况下,我们知道除数只能是那个原数和1,所以我们可以立即返回它们。
return (1,N) if factors.total == 1;
.total 方法只是简单地将袋子里所有的整数权重相加。如果总和为1,则只能有一个元素,权重为1。
否则,袋子中的一个或多个键(factors.keys)就是原数的质因子列表(pₗ,pₘ,pₙ,...),我们提取这些质因子并存储在一个合适的 Unicode 命名的变量中:pₗpₘpₙ。请注意,我们需要多个相同的初等因子列表副本:每一个可能的指数组合都需要一个。由于我们还不知道(还不知道)会有多少这样的组合,为了确保我们有足够的数量,我们只需将列表无限长:factors.keys xx ∞。在我们的例子中,这将产生这样的因子列表:
((1,3,5,17,379721), (1,3,5,17,379721), (1,3,5,17,379721), ...)
为了得到指数集的列表,我们需要每一个可能的指数组合(I,J,K,…),从零到每个素数的最大数。也就是说,对于我们的例子来说:
{ 2=>1, 3=>2, 5=>1, 17=>2, 379721=>1 }
我们需要:
( (0,0,0,0,0), (0,0,0,0,1), (0,0,0,1,0), (0,0,0,1,1), (0,0,0,2,0), (0,0,0,2,1),
(0,0,1,0,0), (0,0,1,0,1), (0,0,1,1,0), (0,0,1,1,1), (0,0,1,2,0), (0,0,1,2,1),
(0,1,0,0,0), (0,1,0,0,1), (0,1,0,1,0), (0,1,0,1,1), (0,1,0,2,0), (0,1,0,2,1),
(0,1,1,0,0), (0,1,1,0,1), (0,1,1,1,0), (0,1,1,1,1), (0,1,1,2,0), (0,1,1,2,1),
(0,2,0,0,0), (0,2,0,0,1), (0,2,0,1,0), (0,2,0,1,1), (0,2,0,2,0), (0,2,0,2,1),
(0,2,1,0,0), (0,2,1,0,1), (0,2,1,1,0), (0,2,1,1,1), (0,2,1,2,0), (0,2,1,2,1),
(1,0,0,0,0), (1,0,0,0,1), (1,0,0,1,0), (1,0,0,1,1), (1,0,0,2,0), (1,0,0,2,1),
(1,0,1,0,0), (1,0,1,0,1), (1,0,1,1,0), (1,0,1,1,1), (1,0,1,2,0), (1,0,1,2,1),
(1,1,0,0,0), (1,1,0,0,1), (1,1,0,1,0), (1,1,0,1,1), (1,1,0,2,0), (1,1,0,2,1),
(1,1,1,0,0), (1,1,1,0,1), (1,1,1,1,0), (1,1,1,1,1), (1,1,1,2,0), (1,1,1,2,1),
(1,2,0,0,0), (1,2,0,0,1), (1,2,0,1,0), (1,2,0,1,1), (1,2,0,2,0), (1,2,0,2,1),
(1,2,1,0,0), (1,2,1,0,1), (1,2,1,1,0), (1,2,1,1,1), (1,2,1,2,0) (1,2,1,2,1)
)
或者,为了更简洁地表达,我们需要每个指数的有效范围的交叉乘积(即 X 算子):
# 2 3 5 17 379721
(0..1) X (0..2) X (0..1) X (0..2) X (0..1)
最大指数只是质数因子袋中的值(factors.value),所以我们可以通过将每个"质数值"转换为 0..count 范围,得到所需指数范围的列表: 0 .. .value for factors。
请注意,在 Raku 中,括号内的循环会产生一个该循环每次迭代的最终值的列表。或者你可以把这个构造看作是一个列表解析,就像在 Python 中一样。[range(0,value) for value in factors.values()](但不那么单调),或者在 Haskell 中,[ [0..value] | value <- elems factors ](但行噪声较小)。
然后,我们只需将得到的范围列表,通过在 X 运算符上还原列表,计算出 n-ary 交叉乘积: [X](0 .. .value for factors),然后将得到的 I,J,K 指数列表存储在一个适当命名的变量中: ᴵᴶᴷ (是的,上标字母是完全有效的 Unicode 字母表,所以我们当然可以用它们作为标识符。)
此时,几乎所有的艰苦工作都已经完成。我们有一个质因数的列表(pₗpₘpₙ),还有一个指数的唯一组合的列表,这些指数将产生不同的除数(ᴵᴶᴷ),所以我们现在需要做的就是用向量指数运算符(pₗpₘpₙ «**« ᴵᴶᴷ) 将第一个列表中的每一个数字集提高到第二个列表中的各种指数集,然后在另一个列表理解中乘以每个指数产生的值列表(([×] .list for …)),产生除数列表。
就这样,就完成了。是五行而不是一行:
multi divisors (\N) {
my \factors = bag prime-factors(N);
return (1,N) if factors.total == 1;
my \pₗpₘpₙ = factors.keys xx ∞;
my \ᴵᴶᴷ = [X] (0 .. .value for factors);
return ([×] .list for pₗpₘpₙ «**« ᴵᴶᴷ);
}
…但里面并没有潜伏着组合式的炸药。我们没有直接建立 O(2ᴺ) 个因子的子集,而是建立 O(N) 个各自指数的子集。
然后我们测试我们更闪亮的新式 divisors 实现。当我们发现它的尺度比之前的好得离谱时,我们会流泪…欣慰。也比原来的试除法好得多:
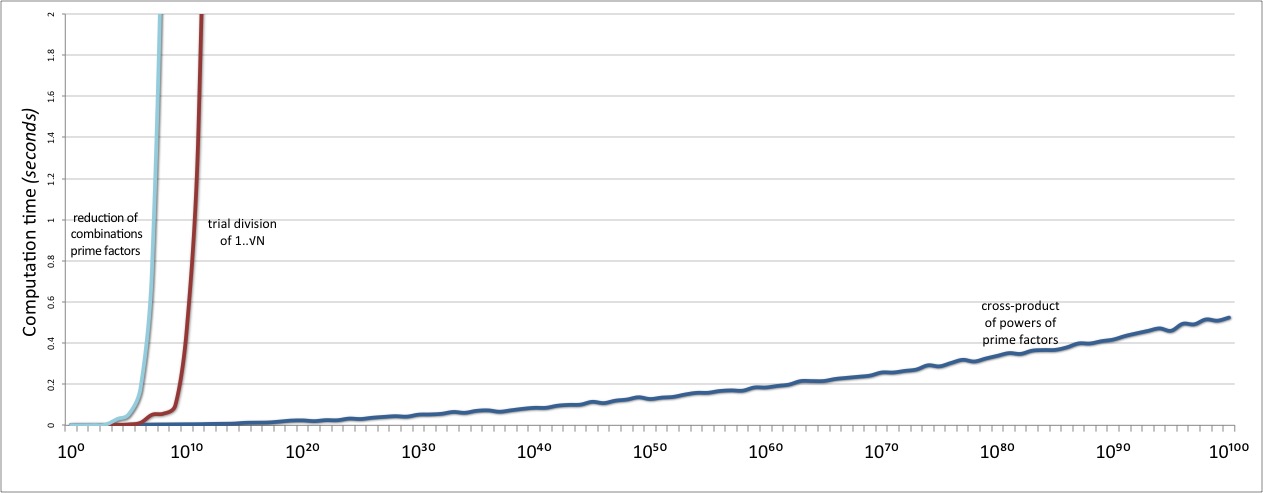
任务完成了!
两全其美 #
只不过,如果我们把图形的起点放大。
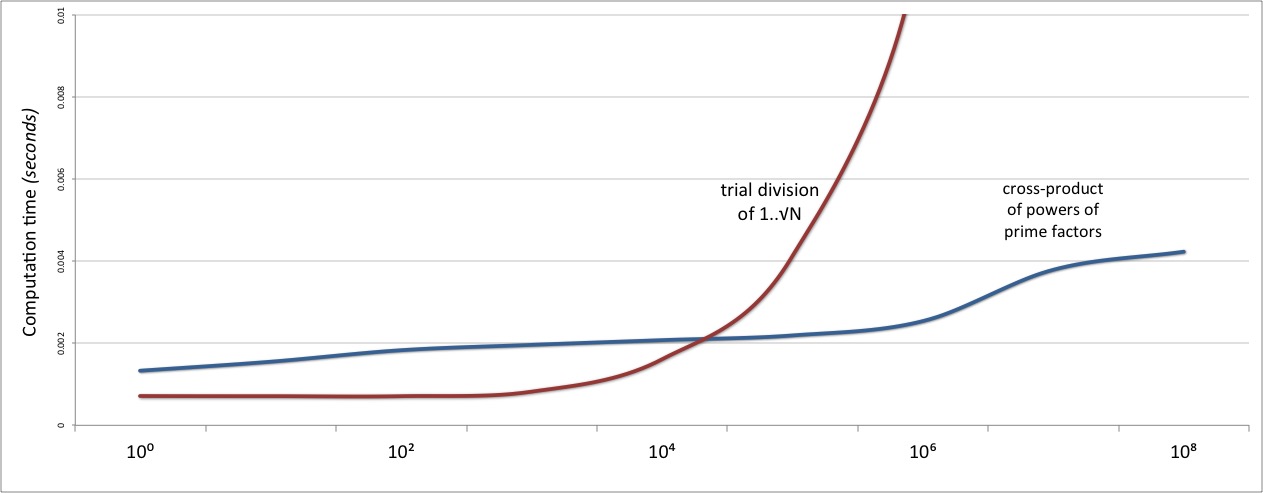
…我们看到,我们新算法的性能最终只会更好。由于 Pollard 的 𝜌 算法的核心计算开销相对较高,而且需要建立、指数化、和质因数的幂集相乘,这个版本的除法的性能比简单的试除法略差……至少在小于 N=10000 的数字上是这样。
理想情况下,我们可以以某种方式同时采用这两种算法:对"小"的数字使用试除法,而对一切更大的数字使用质因数。而这在 Raku 中也是微不足道的。不,不是把它们混在一起,用某种 Frankenstein 函数:
multi divisors (\N) {
if N < 10⁴ {
my \small-divisors = (1..sqrt N).grep(N %% *);
my \big-divisors = N «div« small-divisors;
return unique flat small-divisors, big-divisors;
}
else {
my \factors = bag prime-factors(N);
return (1,N) if factors.total == 1;
my \pₗpₘpₙ = factors.keys xx ∞;
my \ᴵᴶᴷ = [X] (0 .. .value for factors);
return ([×] .list for pₗpₘpₙ «**« ᴵᴶᴷ);
}
}
相反,我们只需像之前那样,在单独的 multi 中独立地实现这两种方法,然后修改它们的签名,告诉编译器它们各自应该应用的N个值的范围:
constant SMALL = 1 ..^ 10⁴;
constant BIG = 10⁴ .. ∞;
multi divisors (\N where BIG) {
my \factors = bag prime-factors(N);
return (1,N) if factors.total == 1;
my \pₗpₘpₙ = factors.keys xx ∞;
my \ᴵᴶᴷ = [X] (0 .. .value for factors);
return ([×] .list for pₗpₘpₙ «**« ᴵᴶᴷ);
}
multi divisors (\N where SMALL) {
my \small-divisors = (1..sqrt N).grep(N %% *);
my \big-divisors = N «div« small-divisors;
return unique flat small-divisors, big-divisors;
}
在这一特殊情况下,实际的改进只是轻微的;也许是太轻微了,不值得为维持两个相同功能的变体而烦恼。但这里所展示的原则是很重要的。Raku 的多重分派机制使得在现有函数中注入特殊情况下的优化变得非常容易…而不会使函数的原始源代码变得更复杂、更慢或更难维护。
同时,在平行宇宙中… #
现在我们有了一个有效的方法来找到任何数字的合适的除数,我们可以使用前面显示的代码开始定位友好对。
for 1..∞ -> \number {
my \friend = 𝑠(number);
say (number, friend)
if number < friend && 𝑠(friend) == number;
}
当我们这样做的时候,我们会发现,前几对数打印出来的速度非常快,但是,之后,事情就开始明显变慢了。所以我们可能会开始寻找另一种方法来加速搜索。
例如,我们可能会注意到,for 循环的每一次迭代都是完全独立于任何其他循环的。不需要外部信息来测试特定的友好对,也不需要在迭代之间传递任何持久状态。而我们很快就会意识到,这意味着这是一个引入一点并发性的绝佳机会。
在许多语言中,将我们简单的线性 for 循环转换为某种并发搜索需要大量的额外代码:调度、创建、协调、管理、协调、同步和终止线程或线程对象的集合。
但在 Raku 中,这只是意味着我们需要在现有的 for 循环中添加一个五字母的修饰符:
hyper for 1..∞ -> \number {
my \friend = 𝑠(number);
say (number, friend)
if number < friend &&𝑠(friend) == number;
}
hyper前缀告诉编译器,这个特定的 for 循环不需要顺序迭代;它的每一次迭代都可以用编译器认为合适的并发程度来执行(默认情况下,以四个并行线程执行,尽管有额外的参数允许你调整并发程度以匹配你的硬件能力)。
hyper前缀实际上只是一个便捷写法,用于在被迭代的列表中添加对 .hyper 方法的调用。该方法将对象的迭代器转换为可以并发迭代的方法。所以我们也可以这样写我们的并发循环:
for (1..∞).hyper -> \number {
my \friend = 𝑠(number);
say (number, friend)
if number < friend &&𝑠(friend) == number;
}
请注意,无论我们以哪种方式写这个并行 for 循环,在多个迭代并行发生的情况下,结果都不再保证严格按照递增顺序打印出来。但实际上,由于整数间友好对的密度较低,无论如何都极有可能出现这种情况。
当我们将之前的 for 循环转换为 hyper for 循环时,循环的性能会翻倍。例如,普通循环可以在一个多小时内找到100万个以内的每一个友好对;hyper 循环则在25分钟内完成同样的工作。
到无穷大,甚至更远 #
最后,在构建和优化了我们寻找失落的情侣的所有组件后,我们可以开始认真地寻找了。不仅仅是寻找第一对友好数,而是寻找第一对超过一千的对,超过一百万的对,超过十亿的对,超过一万亿的对,等等。
# Convert 1 → "10⁰", 10 → "10¹", 100 → "10²", 1000 → "10³", ...
sub order (\N where /^ 10* $/) {
10 ~ N.chars.pred.trans: '0123456789' => '⁰¹²³⁴⁵⁶⁷⁸⁹'
}
# For every power of 1000...
for 1, 10³, 10⁶ ... ∞ -> \min {
# Concurrently find the first amicable pair in that range...
for (min..∞).hyper -> \number {
my \friend = 𝑠(number);
next if number >= friend || 𝑠(friend) != number;
# Report it and go on to the next power of 1000...
say "First amicable pair over &order(min):",
"\t({number}, {friend})";
last;
}
}
这显示:
First amicable pair over 10⁰: (220, 284)
First amicable pair over 10³: (1184, 1210)
First amicable pair over 10⁶: (1077890, 1099390)
First amicable pair over 10⁹: (1000233608, 1001668568)
First amicable pair over 10¹²: (1000302285872, 1000452085744)
et cetera
好吧,最终揭开了他们的面纱!
by Damian